14. FUNCTION Namelist
14.1. Overview
There is often a need to specify phase properties, boundary condition data, source data, etc., as functions rather than constants. The FUNCTION namelist provides a means for defining functions that can be used in many situations.
The namelist can define several types of functions: a multi-variable polynomial, a continuous piecewise linear function defined by a table of values, a smooth step function, and with certain Truchas build configurations, a general user-provided function from a shared object library that is dynamically loaded at runtime. The functions are functions of \(m\) variables. The expected number of variables and what unknowns they represent (i.e., temperature, time, x-coordinate, etc.) depends on the context in which the function is used, and this will be detailed by the documentation of those namelists where these functions can be used.
Polynomial Function This function is a polynomial in the variables \(v = (v_1,.....,v_m)\) of the form
with coefficients \(c_j\), integer-valued exponents \(e^{ij}\), and arbitrary reference point \(a= (a_1,...,a_m)\). The coefficients are specified by Poly_Coefficients, the exponents by Poly_Exponents, and the reference point by Poly_Refvars.
Tabular Function This is a continuous, single-variable function \(y = f(x)\) interpolated from a sequence of data points \((x_i,y_i), i= 1,...,n,\) with \(x_i < x_i+1\). A smooth interpolation method is available in addition to the standard linear interpolation; see Tabular_Interp. There are also two different methods for extrapolating on \(x < x_1\) and \(x > x_n\); see Tabular_Extrap.
Smooth Step Function This function is a smoothed \((C_1)\) step function in a single variable \(v= (x)\) of the form
with parameters \(x_0\), \(x_1\), \(y_0\), and \(y_1\)
Shared Library Function This is a function from a shared object library having a simple Fortran 77 or C compatible interface. Written in Fortran 77 the function interface must look like
double precision function myfun (v, p) bind(c)
double precision v(*), p(*)
where myfunc can, of course, be any name. The equivalent C interface is
double myfun (double v[], double p[]);
The vector of variables \(v= (v_1,...,v_m)\) is passed in the argument \(v\) and a vector of parameter values specified by Parameters is passed in the argument \(p\). Instructions for compiling the code and creating a shared object library can be found in the Truchas Installation Guide. The path to the library is given by Library_Path and the name of the function (myfun, e.g.) is given by Library_Symbol. Note that the bind(c) attribute on the function declaration inhibits the Fortran compiler from mangling the function name (by appending an underscore, for example) as it normally would.
14.2. FUNCTION Namelist Features
14.3. Components
Name
Type
Library_Path
Library_Symbol
Parameters
Poly_Coefficients
Poly_Exponents
Poly_Exponents(i,j) = .....
defines the value for exponent \(e_{ij}\). All the variable exponents for coefficient \(j\) can be defined at once by listing their values with the syntax
Poly_Exponents(:,j) = .....
In some circumstances it is possible to omit providing 0-exponents for variables that are unused. For example, if the function is expected to be a function of (t,x,y,z), but a polynomial in only t is desired, one can just define a 1-variable polynomial and entirely ignore the remaining variables. On the other hand, if a polynomial in z is desired, one must specify 0-valued exponents for all the preceding variables.
Poly_Refvars
Tabular_Data
Tabular_Data(1,:) = x_1, x_2, ......., x_n
Tabular_Data(2,:) = y_1, y_2, ......., y_n
specifies the \(x_i\) and \(y_i\) values as separate lists. Or the values can be input naturally as a table
Tabular_Data = x_1, y_1
x_2, y_2
...
x_n, y_n
The line breaks are unnecessary, of course, and are there only for readability as a table.
Tabular_Dim
Tabular_Extrap
Tabular_Interp
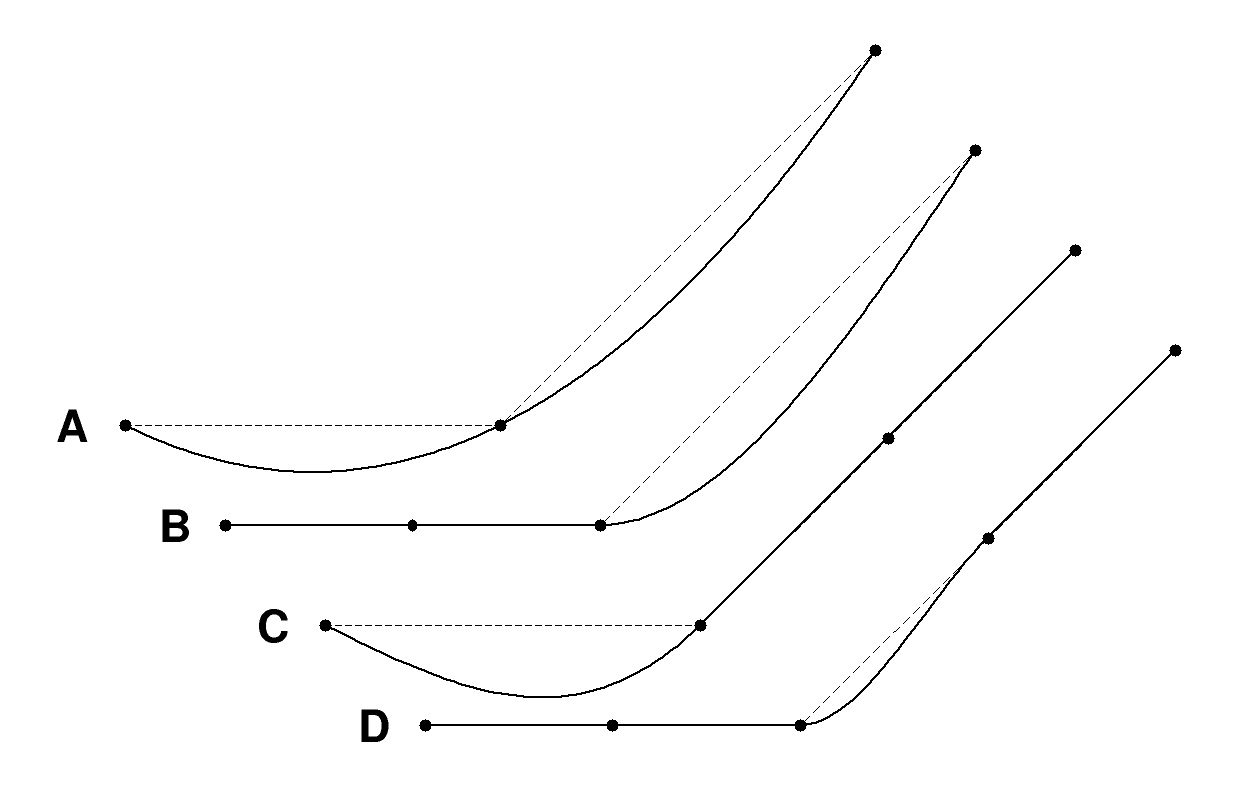
Figure 14.3.1 Examples of smooth Akima interpolation.